Although the database and the data model are at the heart of the Django web framework, as a Django developer it's actually fairly unusual to you find yourself writing SQL to talk to your database directly. Most database queries happen through Python calls to Django's ORM, using the powerful and flexible QuerySet API. This makes code easier to read and maintain, safer, faster to write, and portable across different database backends. All good things.

It also means that when you do find yourself writing raw SQL, it's usually for something quite interesting or challenging. So a Django developer would be well advised to keep their SQL skills sharp --- you might get away with writing Django without much SQL knowledge for a little while, but that will only hold good right up to moment when you hit a particularly hard problem that you can't solve with the ORM. The ORM handles the ordinary, workaday queries. The exotic and interesting stuff you have to write yourself.

Occasionally those moments provide an opportunity for you to really learn something new about SQL and databases. In this post I'll share something I learned after we had to write an unusual raw SQL query for a project here at Fusionbox. The query was what's known in database-land as a Recursive Common Table Expression (Recursive CTE) --- a rarely-used device, but one of some deep computational power and significance, as it happens to be the magic ingredient that makes SQL Turing Complete. To illustrate what the Recursive CTE is capable of, we'll make some brief forays into graph traversal and sorting algorithms and how these can be implemented in SQL to make queries about the structure of complex foreign key relationships.

Databases and Graphs

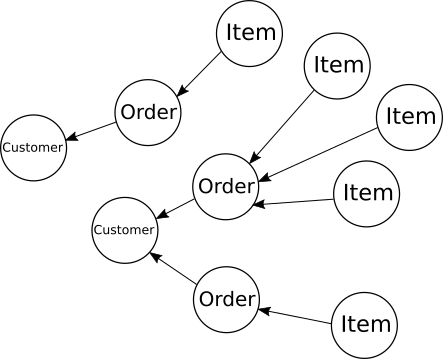
Look at a database from the right angle, and you'll see a graph. That's a graph in the mathematical graph theory sense of set of objects (vertices) connected by relationships (edges). For a database the vertices are the rows of tables and the edges are the foreign key relationships between them. Most of the time those graphs don't have a tremendously interesting structure. For example, if we have a foreign key relationship between (say) three tables, 'customer', 'order', and 'item', where order has a foreign key to customer and item has a foreign key to order, then our database graph won't have any path longer than 2 edges (an item->order->customer relationship):

Sometimes, however, you might have a much more interesting foreign key structure. Here's an example: task scheduling. Say you're managing a large project, and you have a list of tasks which have dependencies on each other, meaning that some tasks cannot start until others have been completed. Let's assume (for now) that each task can only have one direct parent - i.e. for each task we can only specify one task which our task directly depends upon. That's an unrealistic assumption for real tasks, but we'll deal with the general case later. If we make this assumption, we can represent the relationship by giving the task table a 'dependent_id' foreign key to another row in the task table:

CREATE TABLE task (
id INT PRIMARY KEY,
dependent_id INT REFERENCES task
);

Ordinarily there would be some other data on the task table as well (at the very least, a name), but I'm leaving that off for simplicity as it doesn't affect the structure of the graph.

If you don't have Postgres installed and want to quickly play with the SQL yourself, I highly recommend http://sqlfiddle.com (make sure you choose the Postgres setting).

In this case, the graph of tasks will be a tree:

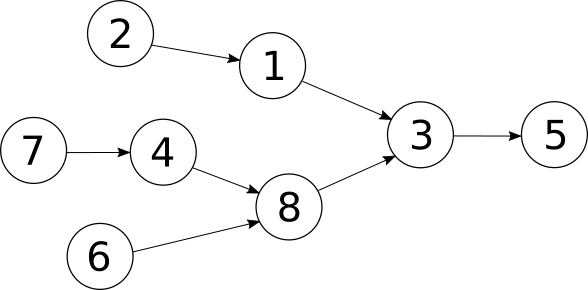
Here, tasks 7, 6 and 2 depend on no other tasks (which would make them a good place to start!), task 8 depends on tasks 4 and 6, and task 3 in turns depends on tasks 8 and 1, etc. I've deliberately labeled the vertices arbitrarily so the labels don't correspond to any ordering in the graph's structure.

You can create this graph of tasks with the following SQL (again, the ordering is deliberately arbitrary):

INSERT INTO task VALUES 
(6, 8),
(3, 5),
(4, 8),
(5, NULL),
(1, 3),
(8, 3),
(2, 1),
(7, 4);

Great, but how do we actually query a construct like this? For example, let's say you want all the tasks that must be completed before you can start task 3. How do you ask the database to give you that information?

The answer, it turns out, is a Recursive CTE (Common Table Expression) - a special type of query that can refer to its own output. Recursive CTEs are an advanced and rarely-used part of SQL, but they can be very powerful. In fact, they are the key ingredient that makes SQL a Turing Complete language, capable of any computation whatsoever (in principle, at least, given infinite memory and time!). In other words, a relational database (provided it supports recursive CTEs) is a universal computing machine. Surprised? Sceptical? Have a look at this SQL to compute and draw the Mandlebrot set fractal.

We'll start out with something more modest: a recursive CTE to traverse our tree of task dependencies to get all the tasks that we'd have to complete before starting task 3. Here's the query to do that:

WITH RECURSIVE traverse AS (
        SELECT id FROM task
        WHERE dependent_id = 3
    UNION ALL
        SELECT task.id FROM task
        INNER JOIN traverse
        ON task.dependent_id = traverse.id
)
SELECT id FROM traverse;

How does this work? Well, first let's look at the structure of the query. Every recursive CTE in Postgres consists of a WITH RECURSIVE clause that contains two SELECT statements, separated by a UNION or UNION ALL. Outside the WITH clause, there's a third select statement that will do something with the result of the recursive CTE. Schematically:

WITH RECURSIVE recursive_table_name AS (
        << Non-recursive SELECT >>
    UNION ALL (or UNION)
        << Recursive SELECT >>
)
<< SELECT from result >>

The core of a recursive CTE is the working table, an intermediate temporary table in the database. The first (non-recursive) SELECT initializes the working table with some rows. The second (recursive) SELECT operates on an expression involving the current working table, and produces a new iteration of the working table. This recursive SELECT repeats over and over again, producing a new iteration of the working table at each step. It stops when the recursive SELECT query finally returns an empty table. The result we get out of the recursive CTE is the UNION ALL (or UNION, if we want to remove duplicates) of all the iterations of the working table - i.e. all their rows appended together to form a single results table.

If that sounded a little confusing, then the best way to understand the process is to see what the working table contains at each step. For our example above to get all the tasks that we'd have to complete before starting task 3, the first non-recursive SELECT statement creates the following working table, containing tasks which have 3 as their dependent id:

id
----
1
8

The first iteration of the recursive SELECT does an INNER JOIN of the working table with the task table to get all the tasks that have tasks 1 and 8 as dependents. We're basically working our way backwards in the tree. The working table now becomes (the order is arbitrary):

id
----
6
4
2

The next iteration of the recursive SELECT does the same thing, but with the above working table as input. The working table is now:

1
2
3

id
----
7

The final iteration of the recursive SELECT gives an empty table as output, because task 7 has no dependents. So the recursion stops.

The result is the UNION ALL of all the working tables:

Ordering and Topological Sort

The recursive CTE we just looked at gets us our list of all the tasks that need to be completed before task 3 can begin. But what if we wanted some kind of ordering on this list --- for example, we might want our tasks list to be in an order in which the tasks could actually be carried out. That order won't be unique (there are several we could choose).

What we're asking for is a special cast of a well-known graph algorithm in computer science: 'Topological Sort'. We'll explore how to do it with SQL for this tree case and then we'll go on to generalize to an arbitrary graph.

Now, it might look like the result table above is already ordered, although as the reverse of what we want: the recursion starts with the tasks just before task 3 and works backwards through the tree. In fact, this is an accident of Postgres's implementation, and no ordering is guaranteed by the recursive CTE. To get that, we have to use ORDER BY on a particular column.

But thinking about how the recursion proceeds back through the tree does give us a hint at how to solve this problem. If we could record the 'depth' of the recursion that corresponds to each row of the output table, then we could order by that depth column (descending) to get a valid topological sort of the tasks. To do that, we simply need to insert a second depth column into our working table for the recursive CTE:

WITH RECURSIVE traverse(id, depth) AS (
        SELECT id, 0 FROM task
        WHERE dependent_id = 3
    UNION ALL
        SELECT task.id, traverse.depth + 1 FROM task
        INNER JOIN traverse
        ON task.dependent_id = traverse.id
)
SELECT id FROM traverse
ORDER BY depth DESC;

The depth column starts out at 0 (in the non-recursive select) and gets incremented at each recursive step. So the successive working tables are:

1:   id | depth 
    ----+-------
      1 |     0
      8 |     0

2:   id | depth 
    ----+-------
      6 |     1
      4 |     1
      2 |     1

3:   id | depth 
    ----+-------
      7 |     2

And the result, ordered by depth descending and selecting the id only, is:

And that's exactly what we want.

Now, suppose we wanted a topological sort of the entire tree, not just those tasks which must be completed before task 3. That is, we want a valid order in which we could complete all the tasks in the task table. All that's needed is a simple modification to the non-recursive part of our CTE: we start by selecting all those tasks which have no tasks depending on them:

WITH RECURSIVE traverse(id, depth) AS (
        SELECT id, 1 FROM task
        WHERE dependent_id IS NULL 
    UNION ALL
        SELECT task.id, traverse.depth + 1 FROM task
        INNER JOIN traverse
        ON task.dependent_id = traverse.id
)
SELECT id FROM traverse
ORDER BY depth DESC;

The output is a valid topological sort of the whole tree.

Incidentally, you might notice we could also do this in reverse, starting by selecting the tasks 2, 7, and 6 (how?) and traversing the tree down towards task 5. If you feel like a challenge, I'd encourage you to try and write that recursive CTE for yourself! Working out how to do it is an important step towards toplogically sorting a generic graph (which we'll do in the next section).

Hint: It turns out it's a lot harder going this direction because you have to deal with duplicate ids. (To understand where the duplicate ids are coming from as the tree gets traversed, it might help to work through each step of the recursive CTE manually.)

Another hint: you'll need to produce some duplicate id output rows from the recursive CTE, then do a GROUP BY and an ORDER BY on the result to convert the output to a topological sort.

Here's my answer:

WITH RECURSIVE traverse(id, depth) AS (
        SELECT task.id, 0 FROM task
        LEFT OUTER JOIN task as t2
        ON task.id = t2.dependent_id
        WHERE t2.dependent_id IS NULL 
    UNION ALL
        SELECT task.dependent_id AS id, traverse.depth + 1 FROM task
        INNER JOIN traverse
        ON task.id = traverse.id
        WHERE task.dependent_id IS NOT NULL
)
SELECT id FROM traverse
GROUP BY id
ORDER BY MAX(depth);

And now the explanation. The non-recursive part selects initial tasks that don't have any other tasks' dependent_ids pointing to them. I did it with a LEFT OUTER JOIN; you could also use a NOT IN or a NOT EXISTS. That gets us the following initial working table:

 id | depth 
----+-------
  2 |     0
  7 |     0
  6 |     0

The recursive part of the query simultaneously traces a path through the graph starting at each of those initial tasks (2, 7, and 6 in this case). Here are the different iterations of the working table after each recursive SELECT:

 id | depth 
----+-------
  1 |     1
  4 |     1
  8 |     1

 id | depth 
----+-------
  3 |     2
  8 |     2
  3 |     2

 id | depth 
----+-------
  5 |     3
  3 |     3
  5 |     3

 id | depth 
----+-------
  5 |     4

The recursive CTE is simultaneously following the three paths through the tree that start at tasks 2, 7, and 6. (2->1->3->5, 7->4->8->3->5, and 6->8->3->5). The first working table corresponds to the first tasks in each of the paths, the second table contains the second tasks, etc. etc. Some tasks appear more than once --- for example task 8 is third in the 7->4->8->3->5 path but second in the 6->8->3->5 path.

How do we get from this to a topological sort? Well, it turns out that if we order by depth and discard all the rows except for only the last time we see a task (i.e. depth = MAX(depth)) we obtain a topological sort! That's what the GROUP BY and ORDER BY are doing at the end of the query above. It might take you a while to satisfy yourself that this always works: try taking a look at task 8 and thinking about how we ensure it always comes after task 4. If you're still not convinced, there's an informal proof in the next section.

Following all the paths might seem quite inefficient[1] compared to our previous approach of starting at node 3 and working back through the graph. But I've taken us down that path because it's a stepping stone to topologically sorting any graph in SQL.

Topological sort of a generic graph in SQL

Earlier, in out task scheduling example, we made the assumption that each task could depend directly on only one other task. That allowed use to represent the data through foreign keys and we ended up with a tree. Obviously, the real world doesn't work like that --- tasks might depend on several tasks. That leads us from a tree of tasks to a general directed graph, where each task vertex may have links to any number of other task vertices. Something like this:

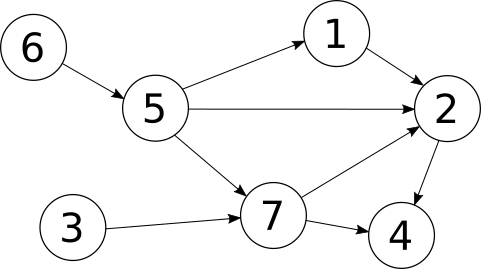
How do we represent that in a database? Well, the edges in a generic graph are a Many To Many relationship between vertices, so we need to use an intermediate 'mapping table' to represent the edges. In the edges table, each row will contain a pair of vertices, the start vertex and the end vertex. Here's some SQL to create the simple graph above:

CREATE TABLE edges (
    start_id INT,
    end_id INT
);

INSERT INTO edges VALUES 
(6, 5), 
(1, 2), 
(5, 1), 
(3, 7), 
(5, 7), 
(7, 2), 
(7, 4), 
(2, 4);

In the real world, start_id and end_id would be foreign keys to some other 'vertices' or 'tasks' table containing the data for each vertex, but since we don't have any data, I've left this out of our example.

For the moment, let's assume that our graph has no cycles (if there is a cycle, then it's impossible to topologically sort the graph --- it would be equivalent in our example to a task depending indirectly on itself!). Then we can use a very similar approach to our last query to obtain a topological sort! The only change is that we need to fix things to use the edges table rather than the id and dependent_id of our task table. (I've also made the recursive step a SELECT DISTINCT to make things slightly more efficient by avoiding following the same path at the same depth more than once.)

WITH RECURSIVE traverse(id, depth) AS (
        SELECT edges.start_id, 0 FROM edges 
        LEFT OUTER JOIN edges AS e2
        ON edges.start_id = e2.end_id
        WHERE e2.end_id IS NULL
    UNION ALL
        SELECT DISTINCT edges.end_id, traverse.depth + 1 
        FROM traverse
        INNER JOIN edges
        ON edges.start_id = traverse.id 
)
SELECT id FROM traverse
GROUP BY id
ORDER BY MAX(depth);

Why does ordering by MAX(depth) always give us a topological sort? Here's an (informal) proof. In a graph with no cycles, we can always identify a set of vertices which have no incoming edges (those are the ones we're selecting in our non-recursive step). Define the 'rank' of a vertex V as the maximum path length from a vertex with no incoming edges (defined to have rank 0) to the current vertex V. This rank or maximum path length always exists because there are no cycles. In fact, it is the same as our MAX(depth) in our query. Now consider two vertices A and B, where B is reachable from A. That means A cannot be reachable from B, otherwise the graph would contain a cycle. Then rank A < rank B. Proof: assume the opposite, i.e. rank A >= rank B. Then because B is reachable from A we can take the longest path to A (length rank A) and extend it to B. That would mean we had constructed a path to B with length > rank B, which is a contradiction. Therefore, if we sort on rank (i.e. MAX(depth)), then because rank A < rank B, we know the following will be true: for all vertices A and B, where B is reachable from A, then A will always come before B in our sort. This is exactly the criterion for a valid topological sort. QED.

The final step to topologically sorting a generic graph in SQL is cycle detection. If there is a cycle, then not only can the graph not be topologically sorted, but our recursive CTE will never terminate! Not something we want happening in our database. Ideally, we'd want to return an empty table in cases where the graph contains a cycle.

This turns out to be kind of hard, and exposes some of the limitations of recursive CTEs. The only way I know of that will do it is to use Postgres's Array data type so that each row stores the full path taken to a vertex. That way we can terminate the path when we encounter a vertex that's already in our path history (which means we've found a cycle). When that happens, we use a special column to set a cycle flag so that we'll know at the end that we hit a cycle somewhere. We can do away with the 'depth' column as that information is now contained in the length of the array in the path column.

The full query is below. It topologically sorts any directed acyclic graph, and returns an empty table when there's a cycle.

WITH RECURSIVE traverse(id, path, cycle) AS (
        SELECT edges.start_id, ARRAY[edges.start_id], false FROM edges 
        LEFT OUTER JOIN edges AS e2
        ON edges.start_id = e2.end_id
        WHERE e2.end_id IS NULL
    UNION ALL
        SELECT DISTINCT edges.end_id, 
               traverse.path || edges.end_id,
               edges.end_id = ANY(traverse.path)
        FROM traverse
        INNER JOIN edges
        ON edges.start_id = traverse.id 
        WHERE NOT cycle 
)
SELECT traverse.id FROM traverse
LEFT OUTER JOIN traverse AS any_cycles ON any_cycles.cycle = true
WHERE any_cycles.cycle IS NULL
GROUP BY traverse.id
ORDER BY MAX(array_length(traverse.path, 1));

Perhaps you can do better. Please tell me if you do.

Warning: Here Be Dragons

Although topologically sorting a generic graph using SQL is a fun challenge, for anything other than small graphs this method would be a bad idea in real code. Why?

Well, our method computes the topological sort by traversing every possible path in the graph that leads from a node with no parents to a node with no children. In the worst case, for dense graphs that have close to the maximum number of edges, the number of paths will be exponential in the number of vertices! (Specifically, O(2^V), assuming no cycles.) Clearly, this isn't going to scale well.

In contrast, implemented in procedural code, topological sort runs in O(V + E) time, where V is the number of vertices and E the number of edges. (Check out Kahn's algorithm, which is my favorite way of doing it.) Worst case, for dense graphs, i.e. E = O(V^2), it will run in O(V^2) in the number of vertices V.

So in fact, unless our graphs were always very small, we'd be much better off doing the topological sort outside the database for a generic graph. The tree example is not exponential and would be safe to use in real code, although I certainly don't guarantee it will perform well when the trees get very large.

Maybe there's a non-exponential SQL query for topological sort, but if so, I haven't been able to find it yet. Either way, the final point stands: it's possible to be too clever. Just because you can compute anything in SQL doesn't mean you necessarily should.

Footnotes:

1 We could make things just slightly more efficient with a SELECT DISTINCT in the recursive step, but that makes it a little less easy to follow so I left it out. And if it was possible to JOIN the working table to previous working tables in the recursive step, then we could do it much more efficiently. But that's not something we're allowed to in a recursive CTE. In fact, Postgres won't even allow us to JOIN a working table to itself in the recursive step!

References:

The Postgres documentation on recursive CTEs was extremely helpful for me coming to grips with this material, and includes an example of tree traversal with cycle detection.

I also learned a lot from talking to colleagues at Fusionbox whose knowledge of Postgres and SQL is deeper than mine. Thanks to everyone who shared their wisdom!

If you, yourself is in need of a Postgres Consulting, Fusionbox provides PostgreSQL development and modeling. We're in Denver, and would love to chat about your project.

Return to Articles & Guides